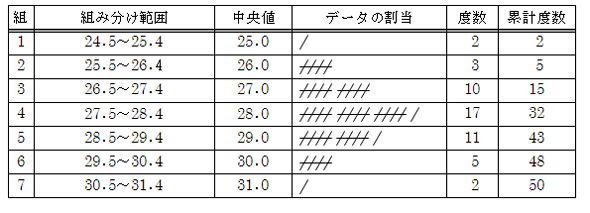
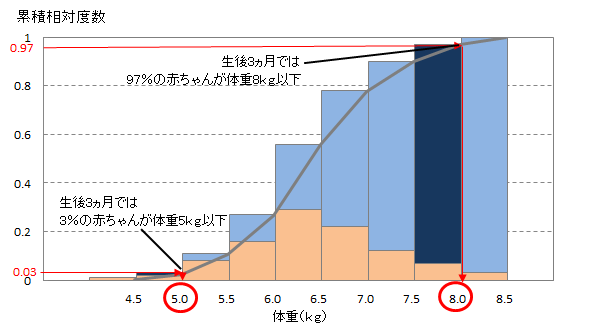
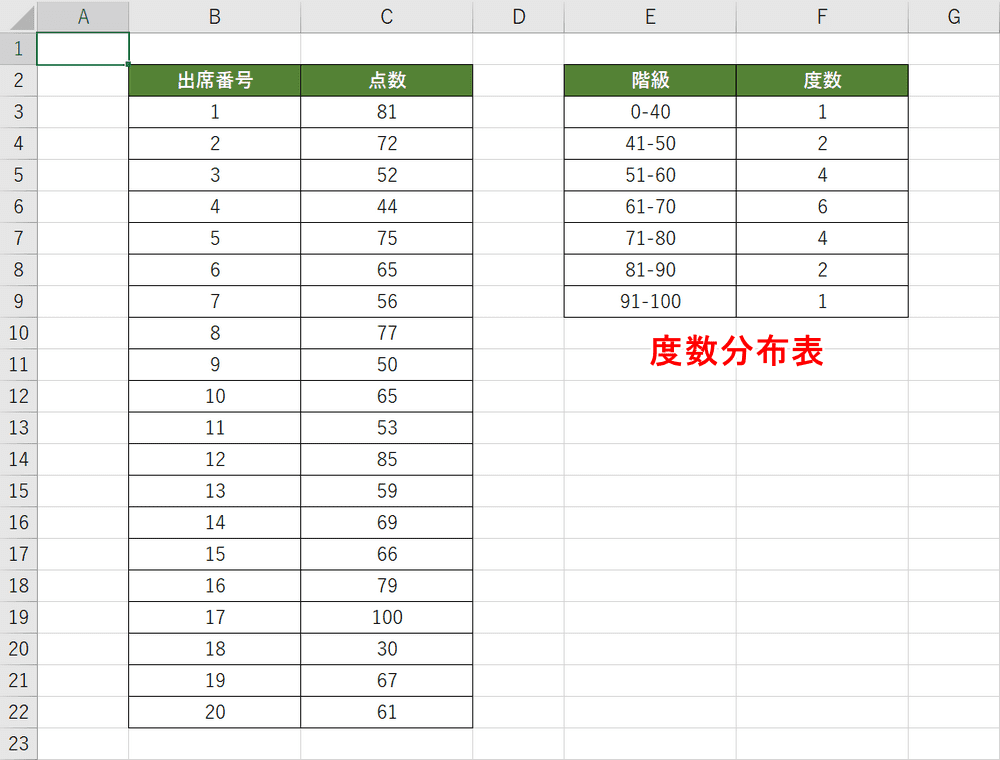
度数分布表 ① 度数分布表の45回以上50回未満の階級の相対度数を求めなさい。 ② 度数分布表から反復横跳びの記録の最頻値を求めなさい。 全国/h29 ⑽ 次の記録は,ある中学校の生徒7人が反復横とびを秒間行ったときの結果を,回数の中央値の近似計算(2) 表2:敷地面積別一戸建住宅数(借家、08年、累積相対度数入り) 資料:総務省統計研修所編(11)『第61回日本統計年鑑』表1817 階級 下限(m 2以上) 上限(m 2未満) 度数(1000戸) 累積相対度数 1 50 214 0111 2 50 75 427 0334動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru
最頻値を求める 中学から数学だいすき
度数 分布 表 中央 値
度数 分布 表 中央 値-中心傾向 平均値、中央値、最頻値、すべての値の合計など、分布の位置を記述する統計です。 Mean (平均) 中心傾向の指標。算術平均 (合計をケース数で割った値) です。 Median (中央値) この値より上と下それぞれにケースの半数ずつが該当することになる値。階級の幅の大きさや度数によって変わってきますが、入試での出題率が上がっているのは個別データより度数分布表の読み取りです。 中央値の求め方 中央値も代表値の\(\,1\,\)つです。 中央値とは、データを小さい順、または大きい順に並べたとき、



医療統計学における度数分布
例 40⼈の歳⼥性の⾝⻑データから作成した度数分布表 「階級値」は境界値の下限と上限の中央の値とする。 各階級の度数を全度数で割った値を「相対度数」とよぶ。 平均は「階級値」×「相対度数」の合計から計算する。 K K K k X X k p k X p X p X p問2 相対度数を 度数分布表 に並べて記 入すると, 右の表のよ うになる。 気温の階級 ℃以上℃未満 度数 相対度数 22~24 24~26 26~28 28~30 30~32 6 6 8 9 1 0 0 027 030 003 計 30 100 2 データの代表値 教科書P164 問3 度数分布表に階級値x と度数f の積xf の欄小学6年生の算数 資料の調べ方|度数分布表・柱状グラフ 練習問題プリント|ちびむすドリル小学生 TOP 小学生の算数 変化と関係・データの活用(数量関係) 練習問題プリント 無料ダウンロード・印刷 小学6年生の算数 資料の調べ方|度数
度数分布表から中央値を求める Last modified Apr 13, 04 目的 度数分布表の形で与えられたデータの 中央値 を求める。 注意:級限界値の取り扱いにより,得られる数値が変わるという微妙な問題がある。 使用法 median2 (f, b, w) 引数 f 度数ベクトル b 最初の階級の開始値 w 階級幅 ソース インストールは,以下の 1 行をコピーし,R コンソールにペーストする source ("http上の記録の中央値は 24 9 (kg) 最 さい 頻 ひん 値 ち (モード) 資料の中でもっとも多く現 れる数値。または,度数分布表で度数がもっと も大きい階級の階級値。 例 上の度数分布表でもっとも度数が大きいのは, 250 kg 以上 26 0 kg 未満の階級であるから,最・度数分布表から平均値を求めると,3 mになる。 など (3) 解答例 ・ハンドボール投げの記録の度数分布表から,この資料の中央値が0 m 第1学年 7 資料の活用
(3) 度数分布表で,各階級のまん中の値を 階級値 かいきゅうち という。例えば,10 分以上 分未満の階 級の階級値は,(10+)÷2=15(分)である。度数がもっとも多いのは 分以上30 分未満の 階級で,その階級値は(+30)÷2=25(分)である。度数分布表1:質的な観測データの要約 データで各々の値の個数(度数)を求める. 度数を表形式にしたものが度数分布表である 着用 非着用 計 有 17 218 235 無 130 428 558 計 147 646 793 頭部損傷 ヘルッメ着用の有無 10 度数分布表2:量的な観測データの要約 id age度数分布表の作成手順 階級数または階級幅を決める 階級値および有効桁数を考え、階級の境界(どこで区切るか)を決める 各階級の度数を数える 階級と度数を元に、度数分布表を作成し、必要に応じて分布の形を見たりする



プログラマーのための統計学 平均値 中央値 最頻値 Qiita



代表値と散らばり Ppt Download
度数分布の下方から累積度数をとって、総度数の半分以上でそれに最も近い累積値 にあたる変数が中央値です。 計算例 F氏宅の60日間の電話の呼数の分布が、次表の通りのとき、 先ず、1日当たりの呼数の、少ない方からの累積度数(日数)を求めます。・メジアン資料の値を大きさの順の並べたときの中央の値のこと。 (中央値)※資料の総数が偶数の場合、中央にある2つの値の平均値。 ・モード 度数が最も多い階級の真ん中の値(階級値)のこと。よって、求める中央値は \(1575(cm)\) です。 度数分布表からの中央値 度数分布表からは、各資料の真の値はわかりません。 よって、階級値を用います。 例1 表は、\(A\) さんの走り幅跳び \(\) 回の記録である。 中央値を求めなさい。 解説



この度数分布表の中央値はどの階級に入るのかおしえてください 1 Yahoo 知恵袋



平均値 Mean 中央値 Median 最頻値 Mode とは何か それぞれの違い 統計学の基礎 統計学の入門サイト 統計ドットリンク
Feb 11, 16 · 度数分布表がある場合で(分かりにくくて申し訳ないですが)、度数が大きい順に2、3、4、4、7と真ん中の数が同じ場合どちらの度数の階級で中央値を求めればいいですか? ※ 4の階級は30〜35(kg)と40〜45(kg)です。個数を対応させた表を度数分布表といい,各階級の中央の値を階級値といいま す(たとえば,この度数分 布表では,階級値は小さい方から, 35,45,55,65, 75,85,95である). また,度数分 布表を柱状のグラフで表したもの をヒストグラムといいます.よって、求める中央値は \(1575(cm)\) です。 度数分布表からの中央値 度数分布表からは、各資料の真の値はわかりません。 よって、階級値を用います。 例1 表は、\(A\) さんの走り幅跳び \(\) 回の記録である。 中央値を求めなさい。



度数分布表とヒストグラム 中卒でも分かる統計学入門 プログラマーになった 中卒 男のブログ



この部品の品質はどれくらい ヒストグラムで見えるもの 実践 Ie 現場視点の品質管理 11 2 2 ページ Monoist
中央値のある階級の、下端を X', 度数を f', 幅を C, X'より下の度数を F',総度数を F とすると、中央値は M e =X'C* (F/2F')/f' (1)Aug 28, · 1度数分布表とは ここでは1次元データの集合から 得られる情報の整理する為、一番 メジャーな度数分布表を見ていきます。 ただし度数分布表は機械学習では ほとんど使われませんが統計学の 基礎を学ぶ為には必要になります。 3平均値・中央値・最頻2.中央値 分布の中心をあらわすために,大きさの順に並べ変えたときに真ん中に位置する観 測値の値を中央値(中位数・median)という 中央値の計算の仕方は、ケース数Nによって異なる ケース数が奇数の場合: (N + 1)/2 番目の値 ケース数が偶数の場合:( N/2



統計学 大学 度数分布表から中央値 Median を求める問 Yahoo 知恵袋



Q Tbn And9gct9g81v6fbuxe2zy40zobgjz7pv4jyf9dpik7xrlwfhfckmjg0k Usqp Cau
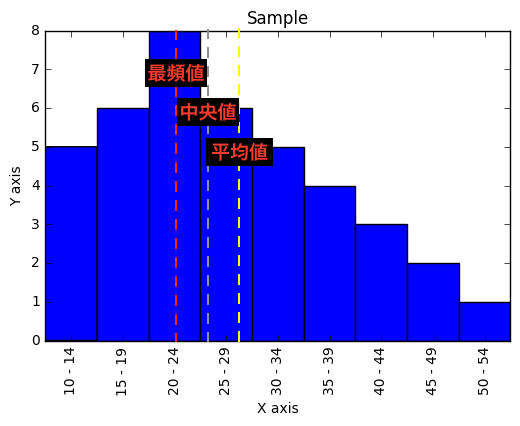
May 02, · 度数分布表と中央値 中央値とは、データを大きさ順に並べたとき、ちょうど真ん中にくる値のことでした。 ちょうど真ん中の値が属する階級の階級値 を中央値とします。平均値 = average(範囲) 2 中央値 (median) これは中間値またはメジアンとも呼ば れ、データを小さい方から大きい方に並べ た、真中の値です。度数分布を用いると、 面積が度数を表わしますので、図51b のよ うに左右の面積の等しい位置が中央値と なります。〇最頻値は,右のような度数分布表として整理された資料に対して考えます. 右の度数分布表において度数の一番多い値 15 が最頻値だと言っているのではありません. 度数が一番多い階級の階級値 525 が最頻値です.



1



度数分布表とは 表の意味と各値の求め方を解説
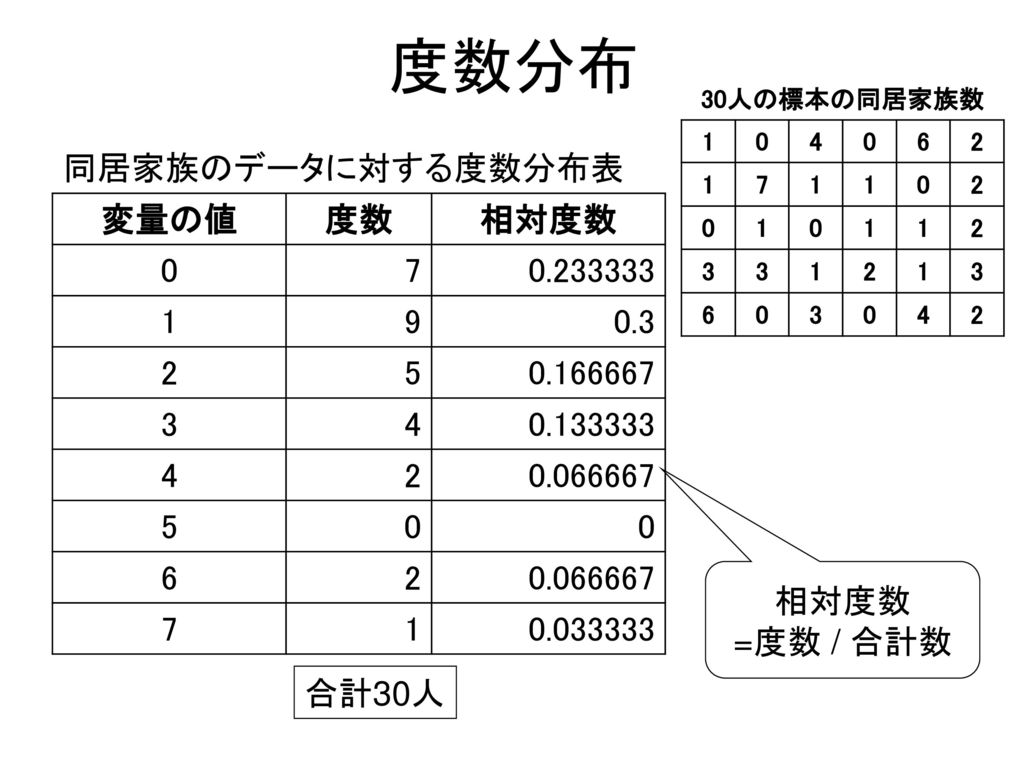
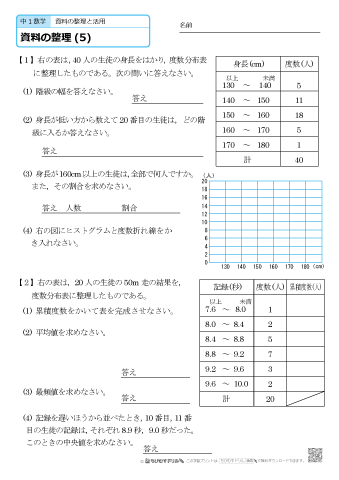
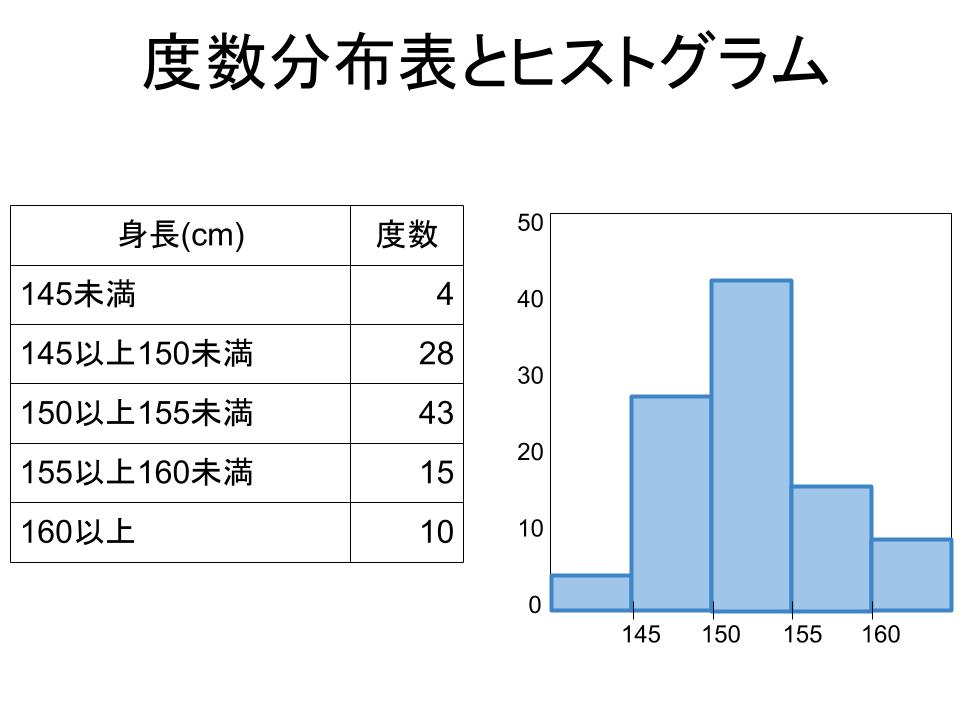
この度数分布表を元にヒストグラムを作ると、次のようになります。 1組のヒストグラムのように山が一つで左右対称の分布の場合、「平均」「 中央値 」「 モード 」はすべて同じ値になります。19Excel#10 ヒストグラムと中央値 株価データの終値について、「 ヒストグラム ( histogram;度数分布) 」 を作成します。 縦軸に度数、横軸に階級(ビン:bin)をとった棒グラフで表した統計 グラフ の一種で、データの分布状況を視覚的に認識するために(3)表の平均値の求め方 度数分布表の各階級値に各人数をかけた値の合計を,人数の合計でわる。 (225 ×1 +275 ×2 +325 ×4 +375 ×8 +425 ×3 +475 ×2)÷ =7300 ÷ =365(cm) 2(1)中央値 <解答例>中央値は資料の値を大きさの順に並べたとき,50番目と51番




度数分布表の意味や見方 数学fun



1
図2 度数分布表ダイアログ・ボックス 平均、標準偏差、中央値、最頻値などの統計量が必要な時には、統計ボタンをクリックし、開かれた度数分布表:統計チェックボックスの必要な統計量(この例では、平均値、中央値、標準偏差)の項目をクリックし、続行ボタンをクリックする。 22版 15版 図3 度数分布表:統計チェック・ボックス デフォルトの出力この度数分布表の中央値はどの階級に入るのかおしえてください 1 Yahoo 知恵袋 度数分布表からの平均値の求め方がわかる5ステップ Qikeru 学びを楽しくわかりやすく度数分布表*棒ギョビ*バシテギョマなど 数値要約 最頻値*中央値*平均値*標準偏差*相関係数など ヅヺソ要約により*必要な情報を簡潔に伝える方法を 記述統計と呼ぶ。 7



度数分布表 健康統計の基礎 健康統計学




データの種類 度数分布表とヒストグラム 統計学基礎
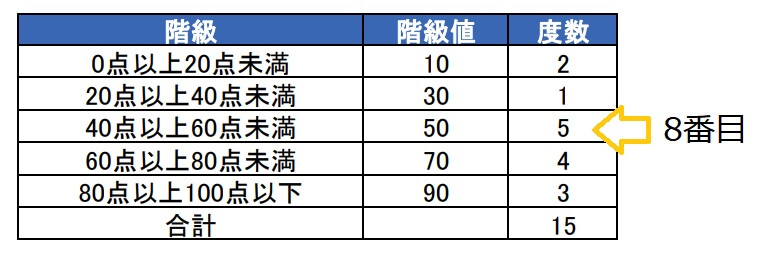
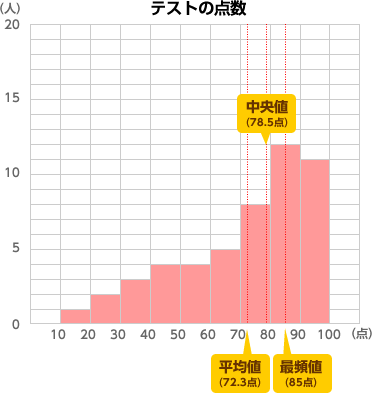
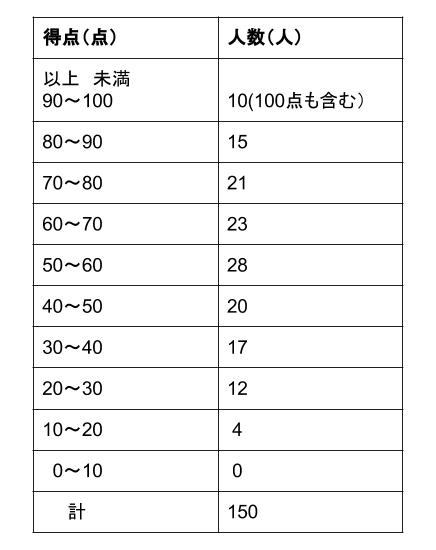
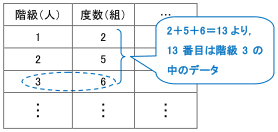
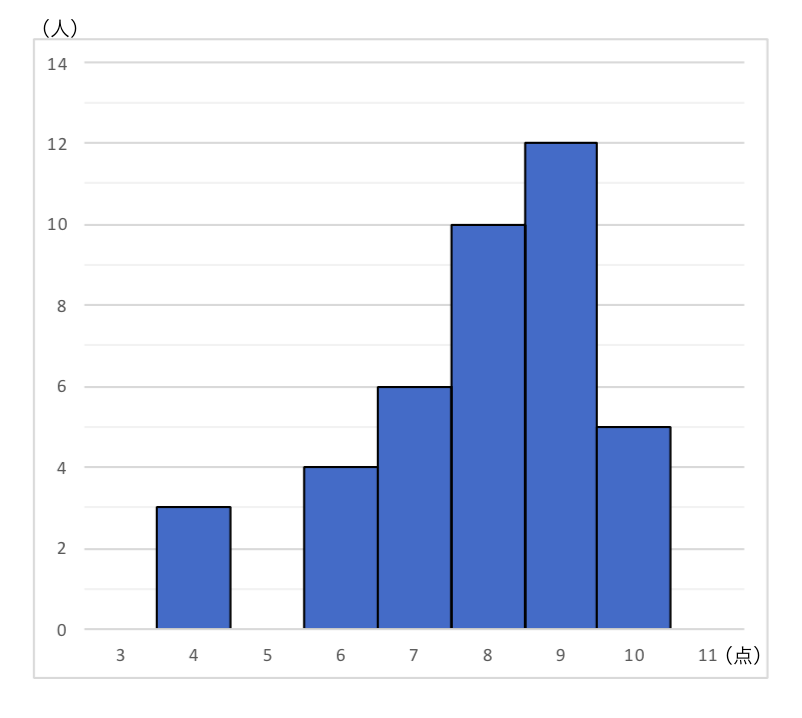
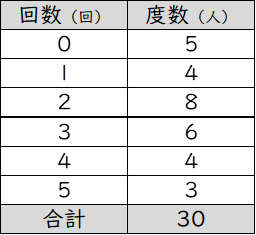
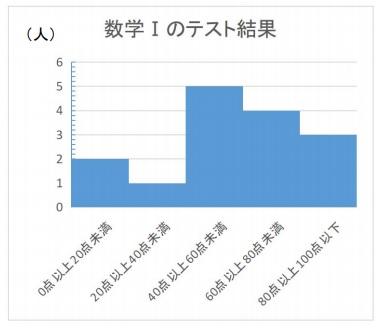
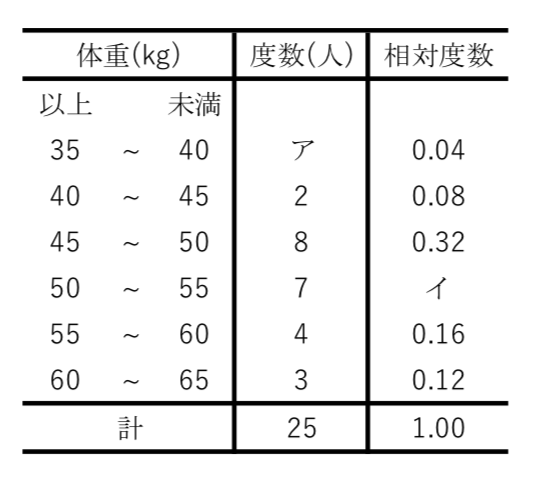
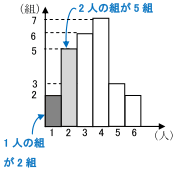
列挙した数値/表/度数分布表:相対度数/累積度数・累積相対度数/最頻値/中央値/ 平均値 /最頻値・相対度数・中央値・平均値など/ヒストグラム/ FdData 入試製品版のご案内 FdData 入試Oct 02, · この度数分布表の中央値の求め方を教えてください 合計が25なので、上から(下から)数えて13番目の値です。 2+5+6=13より、中央値=8~12Feb 22, 21 · まず初めに、中央値とは 「データを小さい順に並べたとき、中央にあるデータ」 のことを指します。 中央値を求めるときには、グラフで考えるよりも、表で考える方が分かりやすいです。 そのため、例題のヒストグラムを表にしたものを下記に示します。 点数 (階級) 人数 (度数



統計解析 第1章 データの表現 Ppt Download




Descubre Como Resolverlo En Qanda
例:ePでePOけみハジタけみタ数値タ平均値ャ計算ガボ =AVERAGE(F1F10) 中央値 中央値ダぎldch`m 関数ャ利用ヵハガく ldch`m(引数ゼ含ハポボ数値タ中央値ャ求ヒボ) 書式Yldch`mG数値PK 数値QKMMMH 引数Y数値PK数値QKMMM:中央値ャ計算ガボけみタ範囲Apr 02, 18 · データの全体の傾向を把握するために「平均値」をよく使うことがありますよね。ただこの平均値、極端に高い・または低いデータがあると、傾向が上振れたり、逆に下振れしてしまうことがあります。 この時活用してみたいのが「中央値」。複数のデータを昇順に並び替えたときに真ん例題: 22 個の測定値がある。中央値を求めよ。 測定値:1,1,2,2,2,2,3,3,3,3,3,3,3,3,4,4,4,4,4,4,5,5 解答:定義からいえば,中央値は 3 であるが,もう少しましな推定値を求めよう。 まずデータ整理のために度数分布表を作



まなぼう統計 統計を知ろう 学ぼう データの特徴 変化をとらえよう 資料のちらばりを表す 代表値




度数分布 ヒストグラム 相対度数 平均値 代表値 無料で使える中学学習プリント
度数分布表からの平均値の(だいたいの)求め方 階級値 度数をすべて加えて, データの総数で割る 階級 階級値 度数 階級値 度数 145 より大きく150 以下 7 150 より大きく155 以下 17 155 より大きく160 以下 29 160 より大きく165 以下 19例えば「1, 1, 2, 4, 5, 8, 9, 10, 11」というデータの場合、中央値は「5」です。もしデータの数が偶数の場合、例えば「1, 1, 2, 4, 5, 8, 9, 10, 11,14」というデータの場合、中央にある2つの値「5」と「8」の平均が中央値となります。 したがって、中央値は(58)/2=65です。 3 モード(最頻値) モードは最頻値とも呼ばれ、最もデータ数の多い値を指します。例えば「1, 1, 2, 4平均値= 値の合計 資料の総数 度数分布表から平均を求める場合、各階級の資料の値はすべて階級値として計算する。 計算(1475×××××2)÷=1565 中央値を求めよ。 中央値とは資料を大きさの順に並べたときのちょうど真ん中の値




度数分布表とヒストグラム データの整理 の問題を解ける 数学ia Himokuri




15 30 3 Dfrac4dfracd Descubre Como Resolverlo En Qanda
中央値(メジアン) 順番に並べたとき、真ん中にくる値を中央値(メジアン) と言います。 2 4 3 7 1 5 5 全部で7人だから、 4番目の自分が中央値 14/45 最大値と最小値 代表値とは少し違いますが、グループの中で最大の値 と最小の値も、よく使われます。 最小!




資料のちらばりと代表値 度数分布表からの平均値の求め方 中学数学 定期テスト対策サイト



分布 平均 分散 しまね統計情報データベース




度数分布表から平均値を求める 中学1年の数学 身勝手な主張




例題 累積度数分布表とヒストグラム Youtube




Q A 1 2 A Descubre Como Resolverlo En Qanda
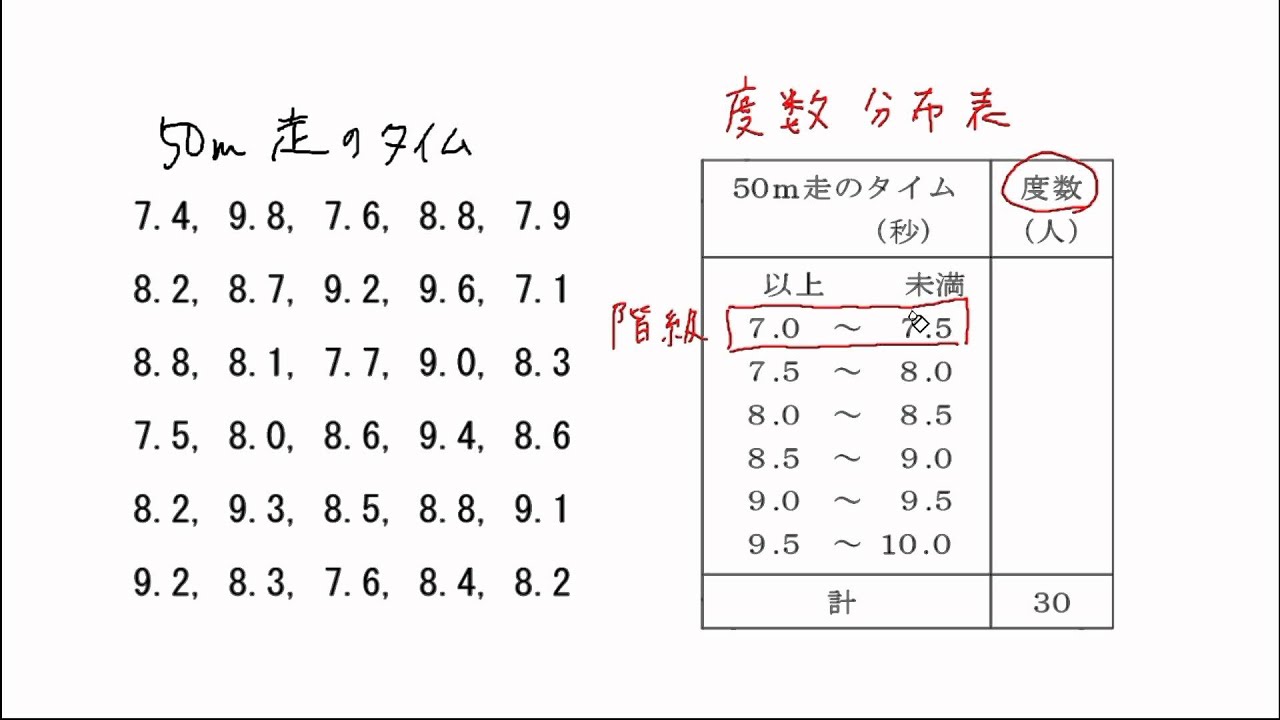



度数分布表 Youtube
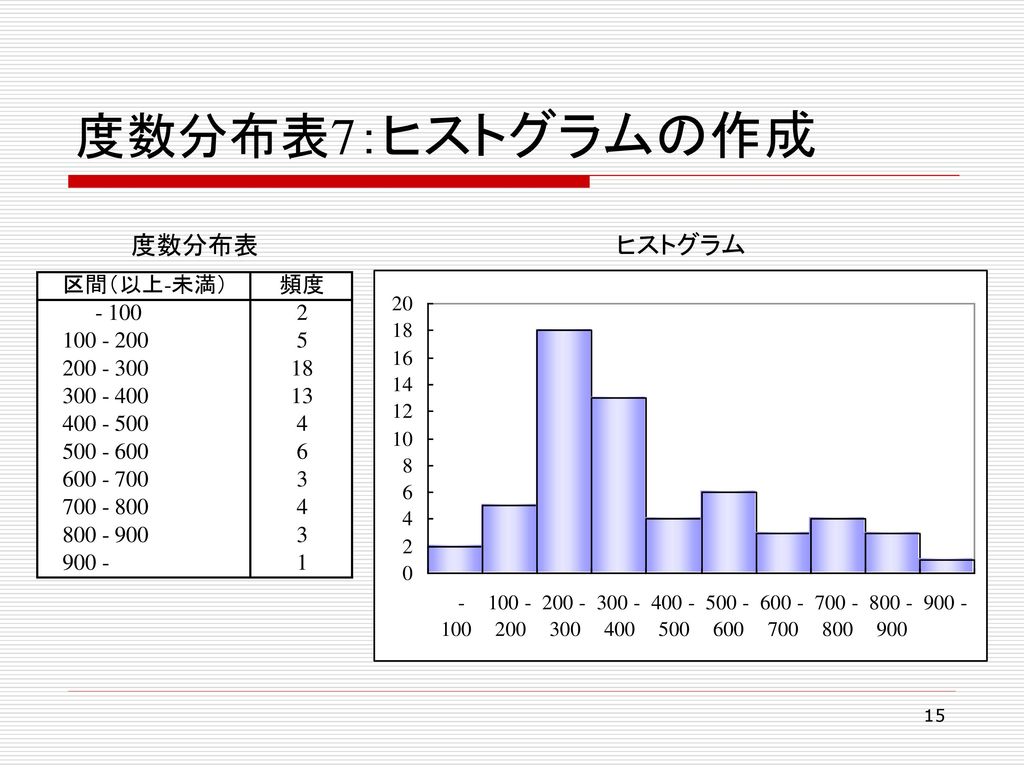



データ解析基礎 2 度数分布と特性値 Keyword データの要約 度数分布表 ヒストグラム 分布の中心を表す基本統計量 Ppt Download



医療統計学における度数分布



1 次のデータは 16人の生徒に100点満点のテストを行った結果を 値 Yahoo 知恵袋



この度数分布表から中央値を求める方法を詳しく教えて欲しいです お願いします Yahoo 知恵袋




小学6年生の算数 資料の調べ方 度数分布表 柱状グラフ 練習問題プリント ちびむすドリル 小学生



Studydoctor階級値と度数分布表での平均の求め方 中学1年数学 Studydoctor




中学数学 3分でわかる 階級値 ってなに Qikeru 学びを楽しくわかりやすく
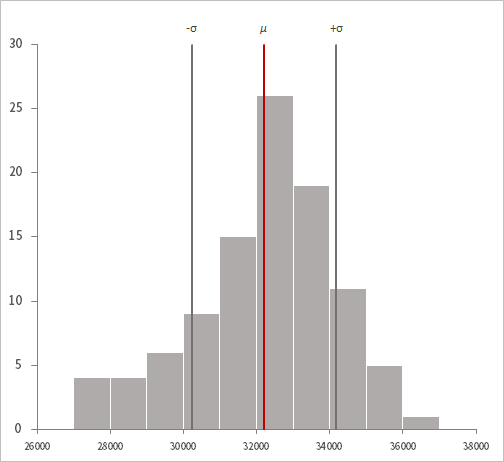



Excelによるヒストグラム 作図のためのtips 平均 規格値などの垂線を重ねる



最頻値を求める 中学から数学だいすき




度数分布表とヒストグラム Youtube



3 2 平均 中央値 モードの関係 統計学の時間 統計web




中1数学 平均値 と 中央値 練習編 映像授業のtry It トライイット
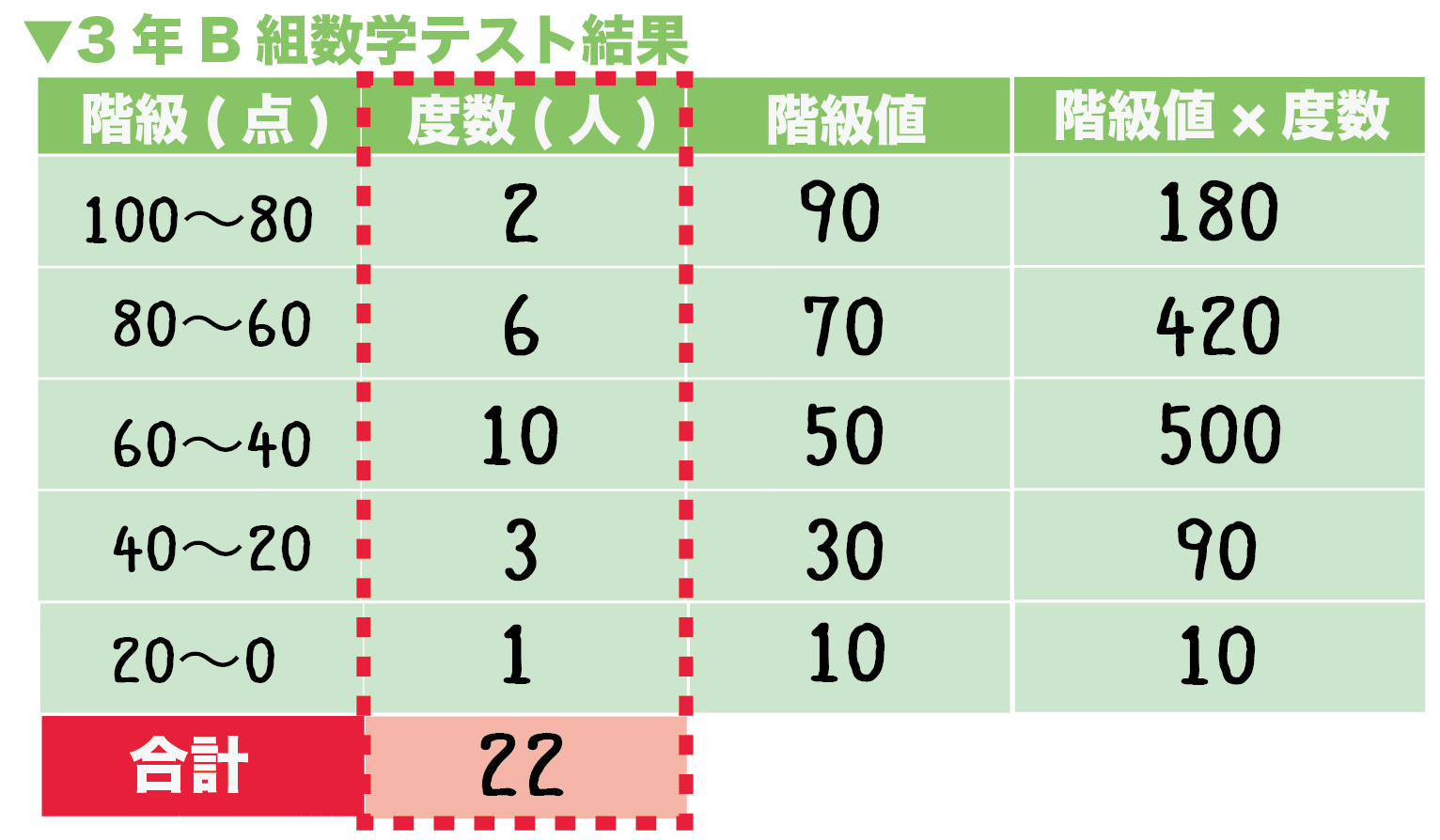



度数分布表からの平均値の求め方がわかる5ステップ Qikeru 学びを楽しくわかりやすく
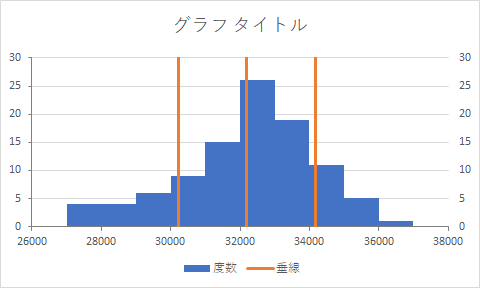



Excelによるヒストグラム 作図のためのtips 平均 規格値などの垂線を重ねる
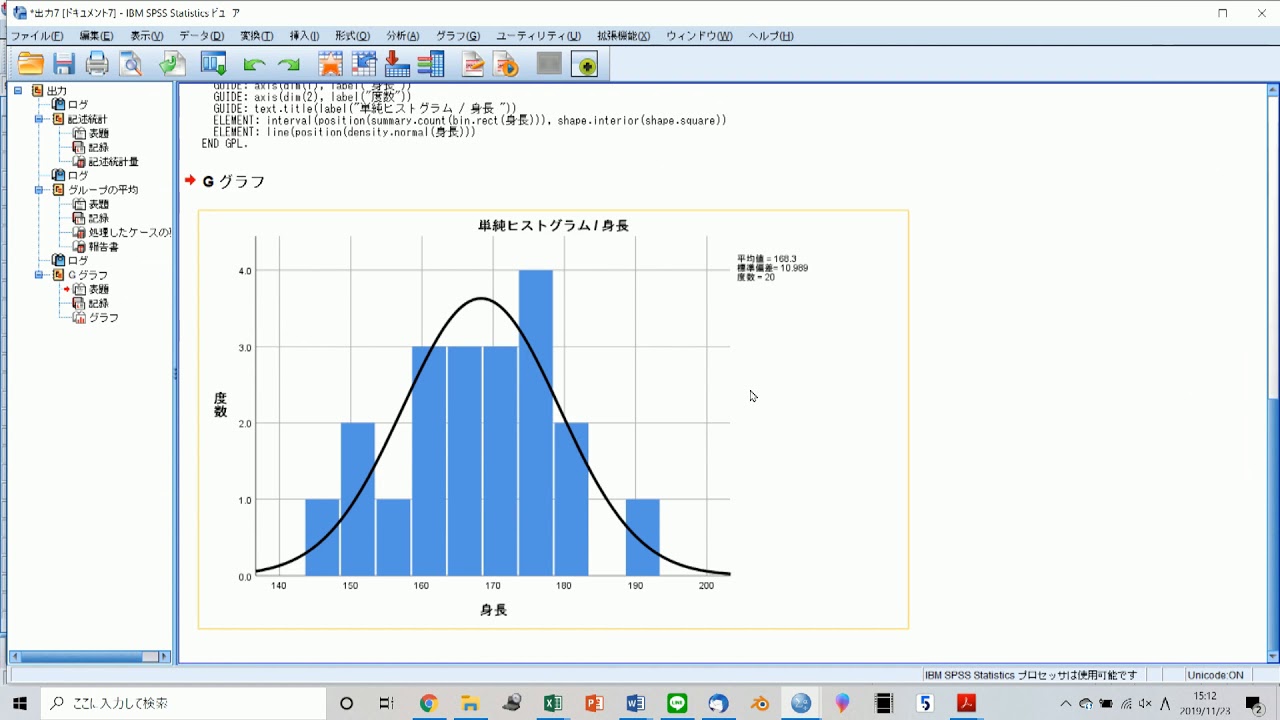



Spssで平均値や中央値 標準偏差 ヒストグラム 散布図 Youtube
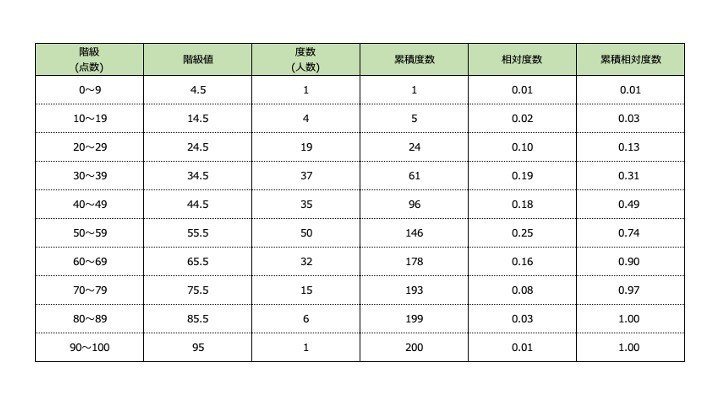



機械学習の統計学 度数分布表 ヒストグラムと平均値 中央値 最頻値について ししまる みらいのクルマをつくる人 Note
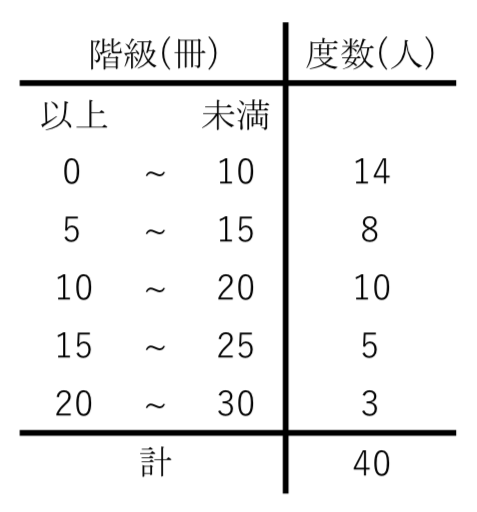



度数分布表から相対度数を求める 苦手な数学を簡単に



中学数学 度数分布表 ヒストグラム 中学数学の無料オンライン学習サイトchu Su



第4回 基礎統計量 2 5 株式会社アイスタット 統計分析研究所



度数分布表から データの傾向を把握しよう かっこデータサイエンスぶろぐ



ヒストグラムとは 作り方 書き方 や階級 データ区間の決め方 受験辞典




第4章 記述統計
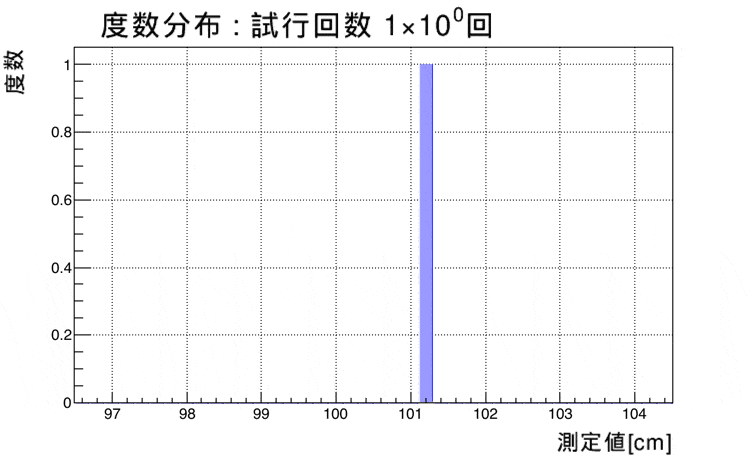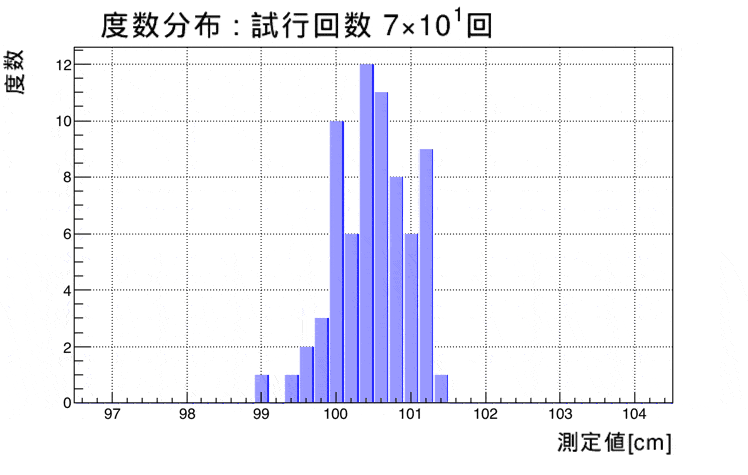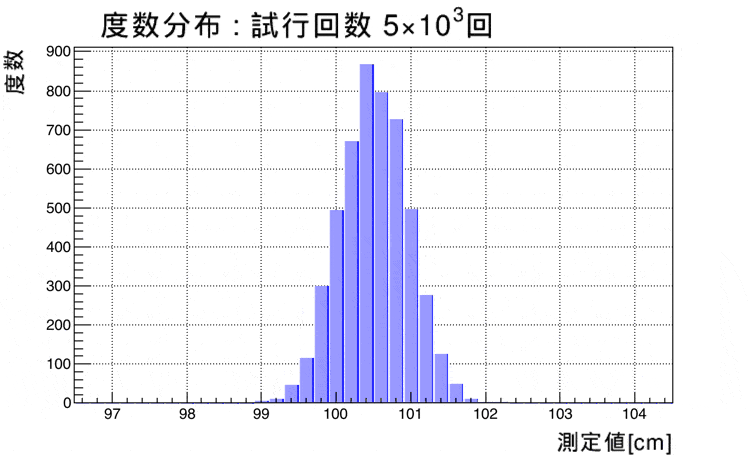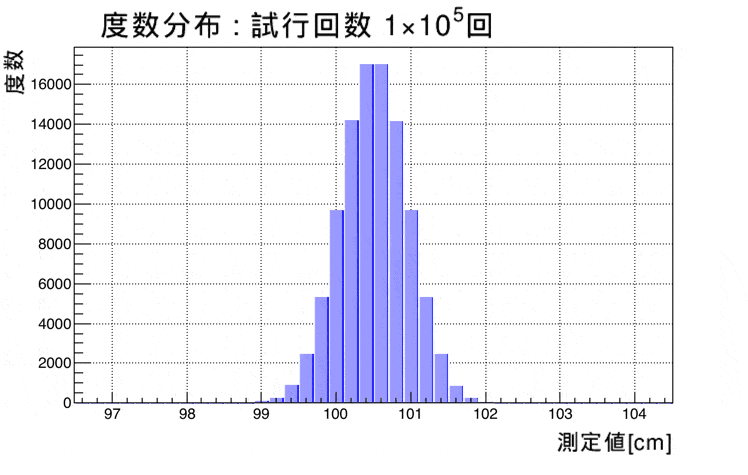



度数分布とヒストグラム 高校物理の備忘録
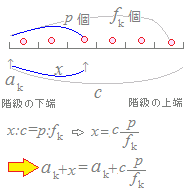



データの代表値 平均値 中央値 最頻値



この度数分布表の中央値の求め方を教えてください 合計が25なので Yahoo 知恵袋




中学数学 資料の散らばりと代表値



ヒストグラムとは エクセルによるヒストグラムの作り方 書き方 Office Hack




数学における度数分布表とヒストグラムとは 中央値 最頻値も 高校生向け受験応援メディア 受験のミカタ



得点源 平均値 中央値 度数分布表 まとめ 中学数学 理科 寺子屋塾の復習サイト




度数分布表から平均値と最頻値を求める 苦手な数学を簡単に
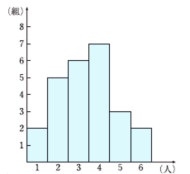



ヒストグラムが与えられたデータから 中央値を求める方法 数学 苦手解決q A 進研ゼミ高校講座
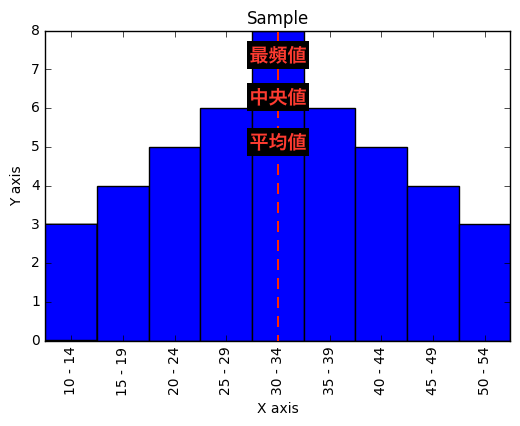



プログラマーのための統計学 平均値 中央値 最頻値 Qiita



ヒストグラムが与えられたデータから 中央値を求める方法 数学 苦手解決q A 進研ゼミ高校講座



中学数学 代表値 中央値 中学数学の無料オンライン学習サイトchu Su



度数分布表の中央値の求め方の問題がわかりません 階級階級値度数 Yahoo 知恵袋



機械学習の統計学 度数分布表 ヒストグラムと平均値 中央値 最頻値について ししまる みらいのクルマをつくる人 Note



ヒストグラムから求める 平均値 中央値 最頻値 苦手な数学を簡単に



数学iib第5問 統計資料の整理 練習用シート




得点の中央値が2点とはどういうことですか Clear
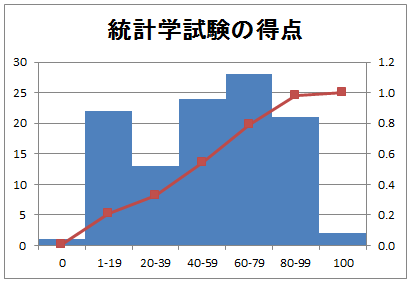



Excelによるヒストグラムの作り方 ブログ 統計web
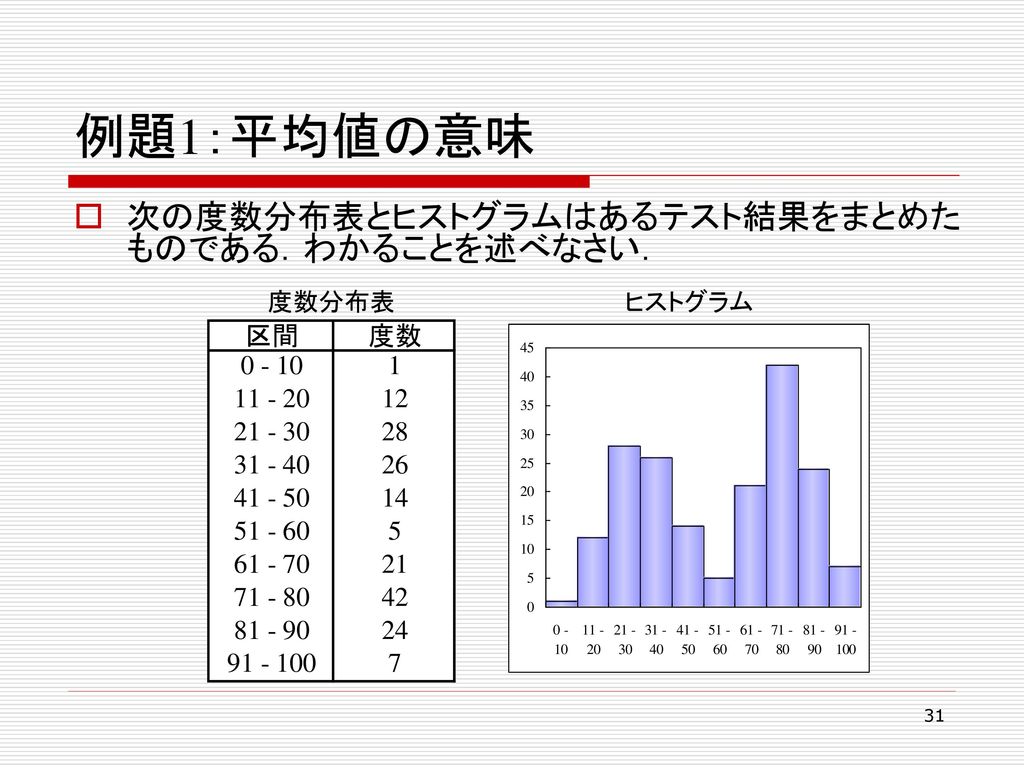



データ解析基礎 2 度数分布と特性値 Keyword データの要約 度数分布表 ヒストグラム 分布の中心を表す基本統計量 Ppt Download
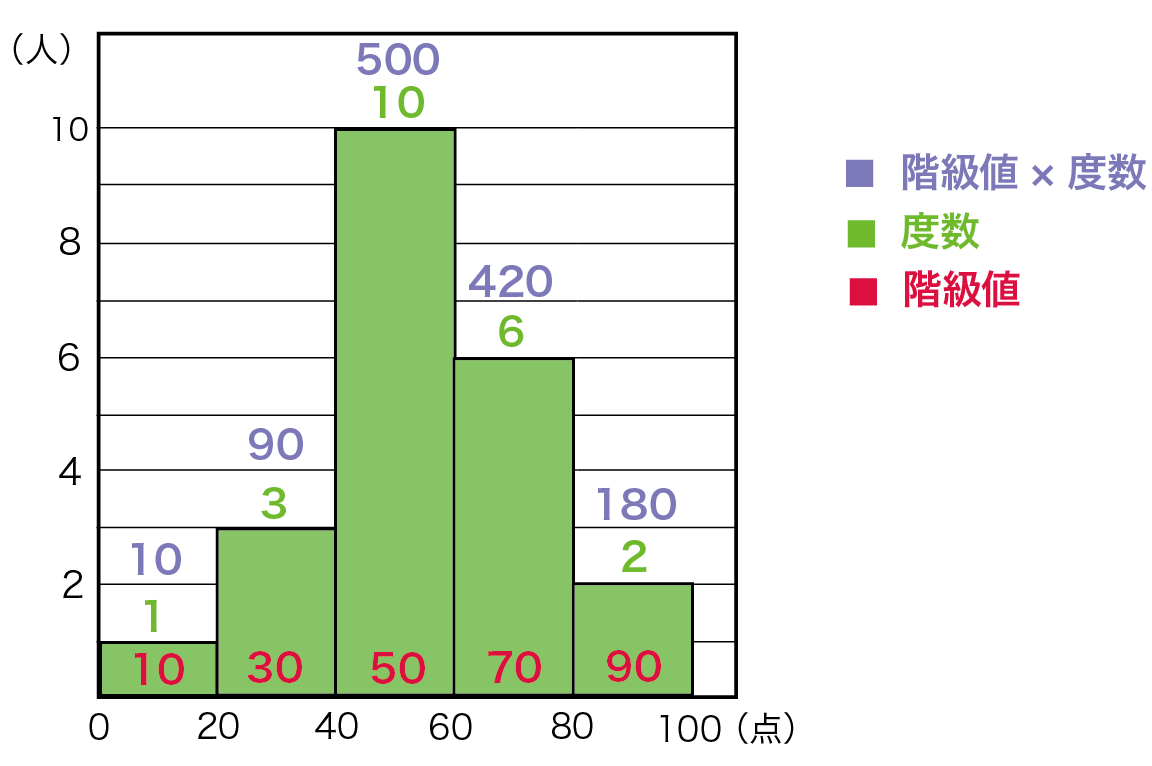



ヒストグラムを使った平均値の求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく
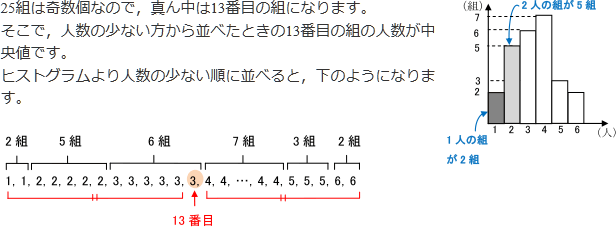



データの分析 ヒストグラムが与えられたデータから 中央値を求める方法 数学 定期テスト対策サイト




中学数学 最頻値 モード の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく



中1数学 資料の整理のポイントと定期テスト予想問題 Pikuu



公立高校入試2015 資料整理 中学から数学だいすき




度数分布表 ヒストグラムとは 作り方 書き方 や特徴などを解説します 遊ぶ数学




代表値 平均値 中央値 最頻値 の意味と違い 数学fun




中央値の求め方と最頻値の求め方を誰か教えて下さい よろしくお願いします Clear



2




機械学習の統計学 度数分布表 ヒストグラムと平均値 中央値 最頻値について ししまる みらいのクルマをつくる人 Note



ヒストグラムをexcelで作成 分析に有効なグラフの作 Udemy メディア




記述統計



中学1年生 数学 資料の整理 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中学数学 中央値 メジアン の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



ヒストグラムの意味と書き方 平均値 中央値の求め方を解説



経営を学ぶ 経営学 Mba 起業
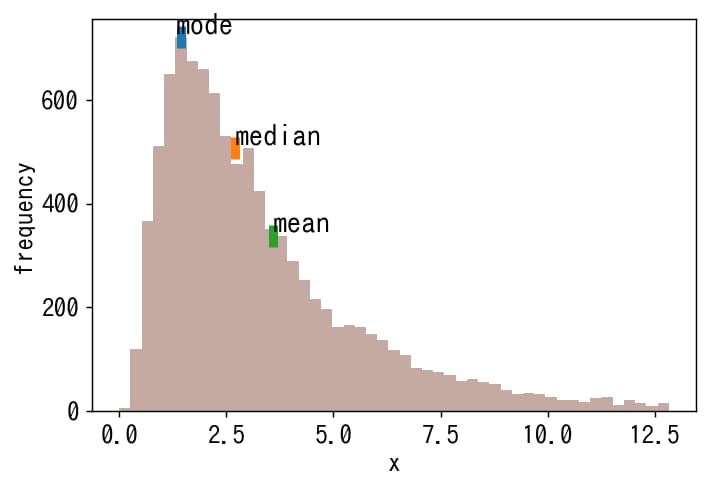



Matplotlib 52 対数正規分布データのヒストグラムに最頻値 中央値 平均値を表示 サボテンパイソン



3 2 平均 中央値 モードの関係 統計学の時間 統計web



度数分布表を完成させよう 求め方は決まっている 苦手な数学を簡単に




中1数学 資料の整理のポイントと定期テスト予想問題 Pikuu



ヒストグラムが与えられたデータから 中央値を求める方法 数学 苦手解決q A 進研ゼミ高校講座
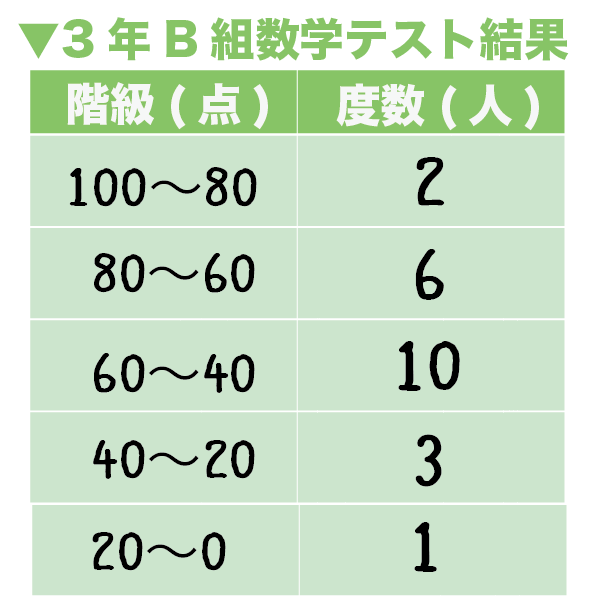



度数分布表からの平均値の求め方がわかる5ステップ Qikeru 学びを楽しくわかりやすく



3 2 平均 中央値 モードの関係 統計学の時間 統計web




中学数学 資料の散らばりと代表値




基礎統計学の勘どころ 1 度数分布表とヒストグラム 箱ひげ図 十の並列した脳




中1数学 資料の整理 度数分布表から最頻値を求める Youtube



わからないです 教えてください 下の度数分布表は ある中学生 Yahoo 知恵袋



中心的な傾向を捉える




中1数学 最頻値 と 階級値 練習編 映像授業のtry It トライイット
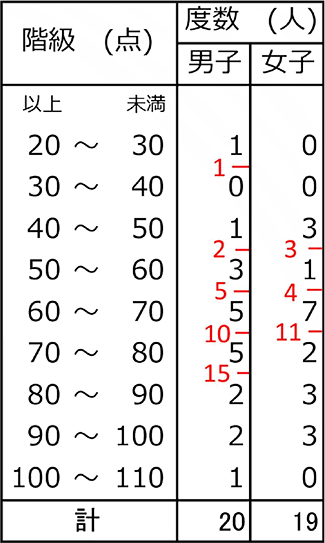



中学数学 資料の散らばりと代表値



中心的な傾向を捉える



1



3 2 平均 中央値 モードの関係 統計学の時間 統計web



ヒストグラム 度数分布からモードを決める場合



度数分布とは 表や多角形の作り方 平均値 中央値 最頻値の問題 受験辞典




19 Excel 10 ヒストグラムと中央値 Johousyori2
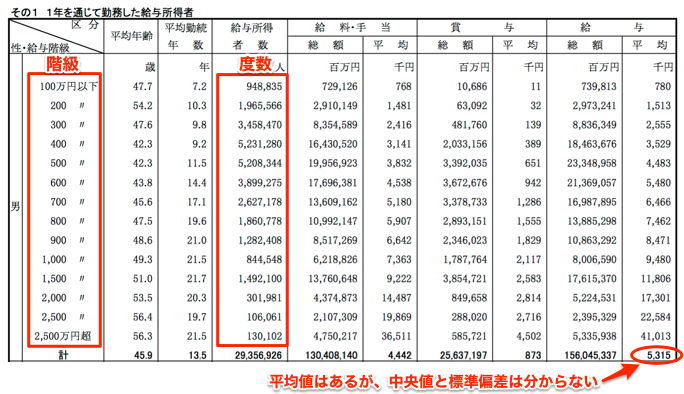



度数分布表からpythonで平均値 中央値 標準偏差を推定する方法 ガンマソフト株式会社


